Module 4: Validating Remote Sensed Data with Ground-Truth Observations

In Module 3, we successfully transformed raw satellite imagery into meaningful environmental variables like NDVI. We now have maps that suggest where vegetation is healthy or where water bodies exist. But a crucial question remains: How accurate are these maps? Do the patterns we see from space truly reflect the conditions on the ground where disease transmission actually occurs?

This module addresses that question head-on. Validation is the process of rigorously assessing the accuracy of our models and maps against independent, real-world data, often called ground-truth data. Without this step, our maps are merely hypotheses. With it, they become evidence-based tools for public health action.

By the end of this notebook, you will be able to: 1. Understand the principle of ground-truthing and its importance in epidemiology.

  1. Link ground-truth data (points) to remote sensing data (rasters) by extracting pixel values.

  2. Perform a formal accuracy assessment for a classified map using a Confusion Matrix.

  3. Calculate and interpret key accuracy metrics like Overall Accuracy, Producer’s/User’s Accuracy (Sensitivity/Specificity), and the Kappa coefficient.

  4. Evaluate models that predict probabilities using Receiver Operating Characteristic (ROC) curves and the Area Under the Curve (AUC).

4.1 Setup: Loading Packages

We’ll use our standard packages, and add two new ones specifically for statistical validation: caret and pROC.

Show/Hide Code 
# install.packages("caret")
# install.packages("pROC")
# install.packages("spDataLarge") # In case you don't have it from Module 3

Now, let’s load our required libraries.

Show/Hide Code 
# Core Packages
library(sf)
library(terra)
library(tmap)
library(dplyr)

# Data Package with a sample satellite image
library(spDataLarge)

# Validation Packages
library(caret)
library(pROC)

4.2 Linking Field Data with Remote Sensing Products

The first step in any validation exercise is to link your ground-truth data to your remote sensing product. This process is called extraction.

Worked Example: Extracting NDVI Values

Let’s imagine we conducted a field survey and have the GPS locations of 100 random survey points. We want to find the NDVI value at each of these locations.

Show/Hide Code 
# 1. Load the landsat raster and calculate NDVI using positional indices
landsat_path <- system.file("raster/landsat.tif", package = "spDataLarge")
landsat <- rast(landsat_path)
landsat_ndvi <- (landsat[[4]] - landsat[[3]]) / (landsat[[4]] + landsat[[3]]) # Using positional indices

# 2. Simulate our ground-truth survey points
set.seed(1984) # for reproducibility
gt_points <- spatSample(landsat_ndvi, size = 100, "random", as.points = TRUE)
gt_points_sf <- st_as_sf(gt_points) %>% # Convert to sf object
    select(-1) %>% # remove the dummy raster value column
    mutate(point_id = 1:100) # Give each point a unique ID

# 3. Perform the extraction
extracted_values <- terra::extract(landsat_ndvi, gt_points_sf)

# 4. Inspect the result
head(extracted_values)
  ID  landsat_4
1  1 0.24296411
2  2 0.09798281
3  3 0.18418055
4  4 0.18159787
5  5 0.11956828
6  6 0.19367867
Show/Hide Code 
# 5. Join the extracted values back to our original points data
gt_points_with_ndvi <- cbind(gt_points_sf, extracted_values)
head(gt_points_with_ndvi)
Simple feature collection with 6 features and 3 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: 304710 ymin: 4113990 xmax: 335040 ymax: 4141110
Projected CRS: WGS 84 / UTM zone 12N
  point_id ID  landsat_4               geometry
1        1  1 0.24296411 POINT (304710 4141110)
2        2  2 0.09798281 POINT (305790 4120380)
3        3  3 0.18418055 POINT (325800 4124700)
4        4  4 0.18159787 POINT (312210 4130640)
5        5  5 0.11956828 POINT (310500 4122330)
6        6  6 0.19367867 POINT (335040 4113990)

4.3 Accuracy Assessment for Classified Maps

To assess the accuracy of a classified map (e.g., “Suitable Habitat” vs. “Unsuitable Habitat”), we use a Confusion Matrix.

Actual: Positive Actual: Negative
Pred: Positive True Positive (TP) False Positive (FP)
Pred: Negative False Negative (FN) True Negative (TN)

Worked Example: Assessing a Habitat Suitability Map

Since we don’t have a real classified map, we will simulate one to understand the methodology.

Show/Hide Code 
# Step 1: Create a more clustered "true" habitat map
set.seed(101)
# Method 1: Using spatial autocorrelation with focal statistics
# Start with random values
true_habitat <- rast(nrows=50, ncols=50, vals=runif(2500))

# Apply multiple rounds of smoothing to create clusters
for(i in 1:3) {
  true_habitat <- focal(true_habitat, w=matrix(1,3,3), fun=mean, na.rm=TRUE)
}

# Convert to binary based on threshold - KEY FIX: convert to numeric
true_habitat <- true_habitat > quantile(values(true_habitat), 0.6)
values(true_habitat) <- as.numeric(values(true_habitat))
names(true_habitat) <- "actual"

# Step 2: Create predicted map with ~20% error
predicted_habitat <- true_habitat
n_errors <- round(ncell(predicted_habitat) * 0.20)
error_cells <- sample(1:ncell(predicted_habitat), n_errors)
predicted_habitat[error_cells] <- 1 - predicted_habitat[error_cells]
names(predicted_habitat) <- "predicted"

# Plot results
plot(c(true_habitat, predicted_habitat), main=c("Actual Habitat (Clustered)", "Predicted Habitat"))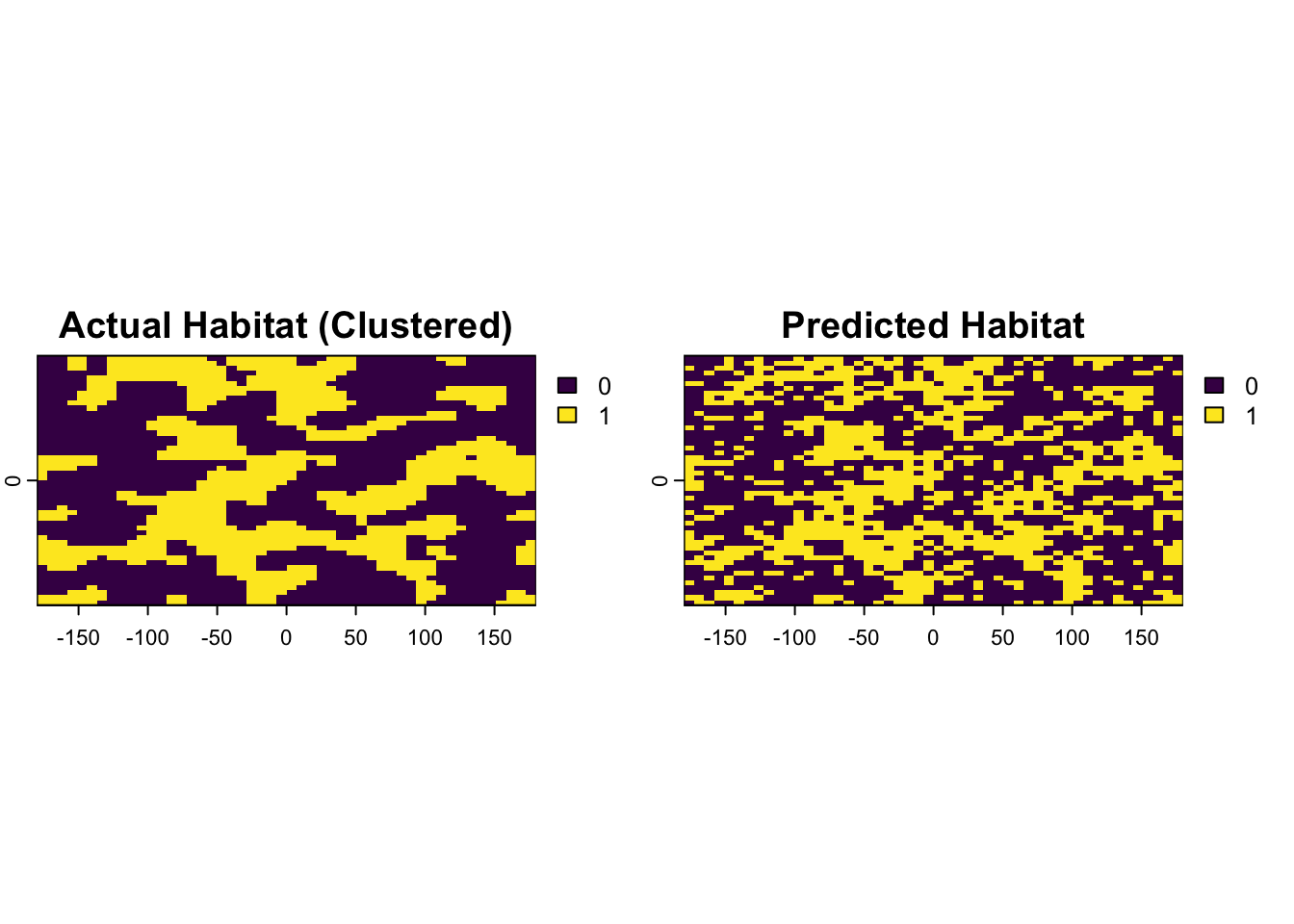

Show/Hide Code 
# Step 3: Generate validation points and extract values
validation_points <- spatSample(true_habitat, size = 250, "random", xy=TRUE)
validation_points$predicted <- terra::extract(predicted_habitat, validation_points[,c("x","y")])$predicted

# Step 4: Prepare data for the confusion matrix
validation_data <- as.data.frame(validation_points)

# Convert to factors - make sure we have 0/1 values first
validation_data$predicted <- factor(validation_data$predicted, levels = c(0, 1), labels = c("Unsuitable", "Suitable"))
validation_data$actual    <- factor(validation_data$actual,    levels = c(0, 1), labels = c("Unsuitable", "Suitable"))

Now we have our validation_data with “predicted” and “actual” columns. Let’s create the confusion matrix.

Show/Hide Code 
# Step 5: Create and interpret the confusion matrix using caret
conf_matrix <- caret::confusionMatrix(data = validation_data$predicted, 
                                     reference = validation_data$actual,
                                     positive = "Suitable")

# Print the full output
print(conf_matrix)
Confusion Matrix and Statistics

            Reference
Prediction   Unsuitable Suitable
  Unsuitable        118       22
  Suitable           26       84
                                          
               Accuracy : 0.808           
                 95% CI : (0.7536, 0.8549)
    No Information Rate : 0.576           
    P-Value [Acc > NIR] : 6.238e-15       
                                          
                  Kappa : 0.6089          
                                          
 Mcnemar's Test P-Value : 0.665           
                                          
            Sensitivity : 0.7925          
            Specificity : 0.8194          
         Pos Pred Value : 0.7636          
         Neg Pred Value : 0.8429          
             Prevalence : 0.4240          
         Detection Rate : 0.3360          
   Detection Prevalence : 0.4400          
      Balanced Accuracy : 0.8059          
                                          
       'Positive' Class : Suitable

4.4 Evaluating Probabilistic Models with ROC Curves

To evaluate models that predict a continuous probability, we use a Receiver Operating Characteristic (ROC) curve. The key summary metric is the Area Under the Curve (AUC), where 1.0 is a perfect model and 0.5 is no better than random chance.

Worked Example: ROC Curve Analysis

Let’s simulate some data for a disease presence/absence study.

Show/Hide Code 
# Step 1: Simulate data
set.seed(42)
n_samples <- 200
roc_data <- data.frame(
  # The true presence (1) or absence (0) of the disease
  ground_truth = rbinom(n_samples, 1, 0.5)
)

# Simulate model probabilities. A good model will give higher scores to the 'presence' cases.
roc_data$model_prob <- ifelse(roc_data$ground_truth == 1, 
                              rnorm(n_samples, mean=0.7, sd=0.2), 
                              rnorm(n_samples, mean=0.3, sd=0.2))
# Ensure probabilities are between 0 and 1
roc_data$model_prob[roc_data$model_prob > 1] <- 1
roc_data$model_prob[roc_data$model_prob < 0] <- 0

# Step 2: Generate the ROC curve object using the pROC package
roc_object <- roc(ground_truth ~ model_prob, data = roc_data)

# Step 3: Calculate the AUC
auc_value <- auc(roc_object)
print(paste("Area Under Curve (AUC):", round(auc_value, 3)))
[1] "Area Under Curve (AUC): 0.922"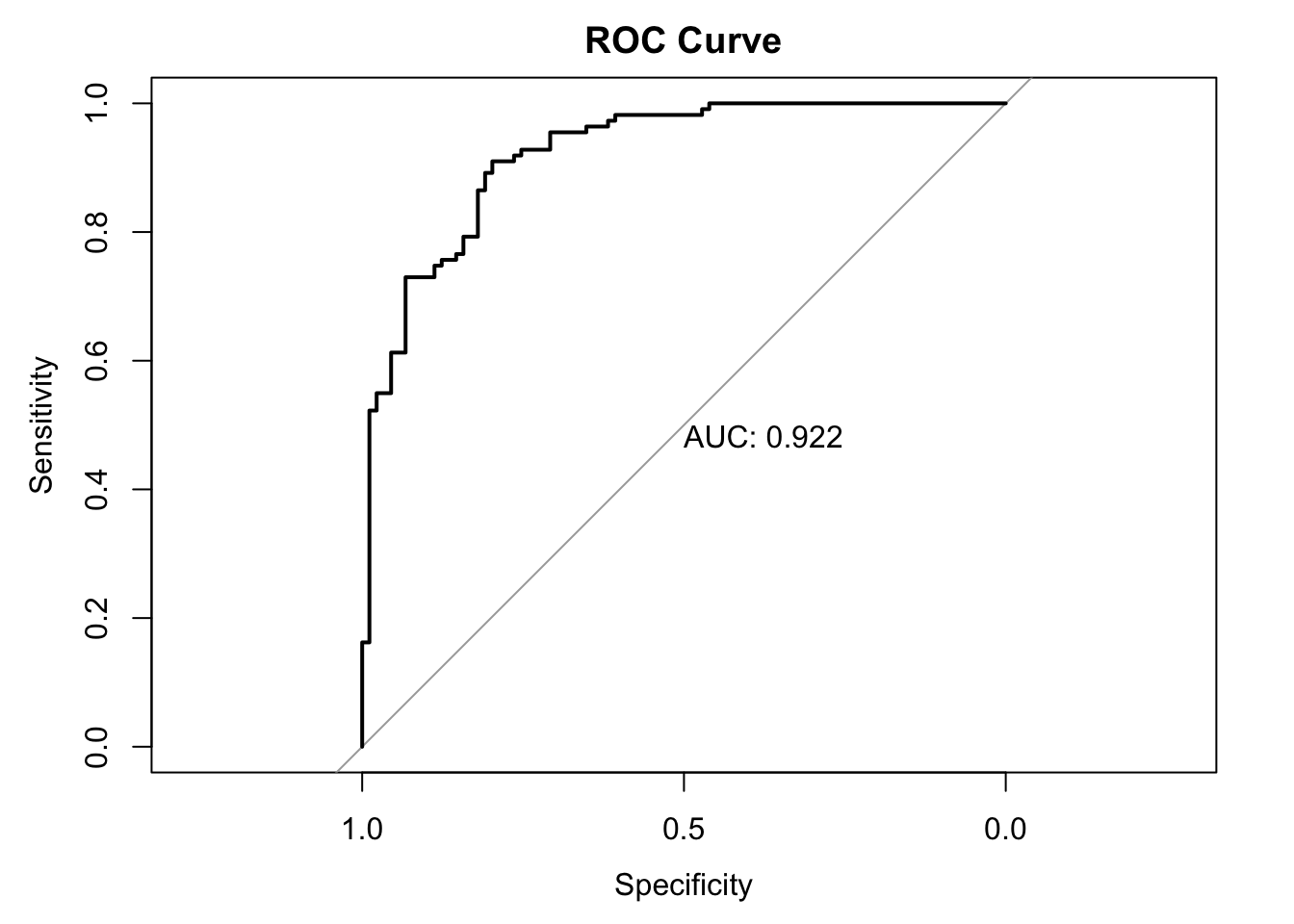
Show/Hide Code 
# Step 4: Plot the ROC curve
plot(roc_object, main = "ROC Curve", print.auc = TRUE)

Our simulated model has an AUC of 0.92, indicating it has excellent discriminatory power.

Module 4 Finish Line

Validation is not just a final step; it is an integral part of the modeling process. In this module, you have learned the essential quantitative methods for evaluating the performance of your geospatial models.

You now know how to link field data to raster data using extraction. You can construct and interpret a confusion matrix and its key metrics to assess a classified map. Furthermore, you can evaluate probabilistic risk models using ROC curves and the AUC.

These skills are what transform a spatial analysis from a descriptive exercise into a rigorous scientific investigation. They allow you to quantify the uncertainty in your results and provide the evidence needed to have confidence in your findings.

In the next and final modules, we will look at how to build the spatial statistical models themselves and discuss best practices for ensuring your research is robust and reproducible.